Guleixibian2009的个人博客~

最重要的是成就感与精神愉悦。

0%

针、圆周率与……Python?

发表于 更新于 分类于 ，
本文字数： 9.8k 阅读时长 ≈ 9 分钟

万事皆可变，万事亦皆有概率，而偏偏是日常生活中无比普遍的它，有时能创造出一个奇迹。蒲丰投针就恰恰体现了这一点。

一根小小的针，也可以投出整个宇宙。

蒲丰投针实验，本是我们伟长七下的一次数学实验课，课后我将它深化了一下，作为一个编程课题，即“用Python模拟蒲丰投针”。这里用一篇博文，记录一下这次实验课中我的探究成果。

注：写作这篇文章时，我已经八上结束了，故在一些细节可能会有记忆上的偏差，还请谅解。

1. 何谓“蒲丰投针”？

  1. 取一张白纸，在上面画上许多条间距为$a$的平行线。

  2. 取一根长度为$l(l≤a)$的针，随机地向画有平行直线的纸上掷$n$次，观察针与直线相交的次数，记为$m$。

  3. 计算针与直线相交的概率．

布丰本人证明了，这个概率是：

由于它与$\pi$有关，于是人们想到利用投针试验来估计圆周率的值。

布丰发现：有利的扔出与不利的扔出两者次数的比，是一个包含$\pi$的表示式．如果针的长度等于$a/2$，那么扔出的概率为$1/\pi$．扔的次数越多，由此能求出越为精确的$\pi$的值。

2. 纯输出版本与实验的简化

在着手写带有GUI的版本前，我们不妨先对这个实验进行一些简化。我们可以假设这些间距相等的直线都无限长，故这时我们没有必要再去模拟针的x坐标（因为它可以从0取到正无穷，继而没有意义）与纸的宽度，只需要模拟y坐标即可。

2.1 程序初始化

1
2
3
4
5
6
7
8
9
10
11
# -*-Coding:UTF-8-*-
import math, random

lineYlist = [12, 24, 36, 48, 60, 72, 84, 96, 108]

def inRange(n, start, end = 0):
    return start <= n <= end if end >= start else end <= n <= start

print('''This is a Python program to get the approximate value of PI. It simulated the Buffon's needle problem 10 times by dropping 100000 needles each time.
Here we go...
''')

这一段中我们定义了一个列表和一个辅助函数。我这里定义纸的长度为120单位，lineYlist中以12单位为间隔确定了所有的直线y坐标。inRange()这个函数用于判断某个值n是否在start和end之间（且无需考虑start和end的大小关系，可以取等），这在后面会很有用。

2.2 定义Pin类与计算y坐标

如果针的长度等于$a/2$，那么扔出的概率为$1/\pi$．

为了方便计算，我们针的长度取12的一半，6。我们这个Pin类会生成两个参数，y坐标和掉落角度angle，储存在self.coords这个变量里。

1
2
3
4
5
class Pin:
    def __init__(self) -> None:
        # [0]: angle [1]: y1 [2]: y2
        self.coords = [random.randint(0, 180), random.randint(0, 120), None]
        self.angle = self.coords[0]

具体定义如下：

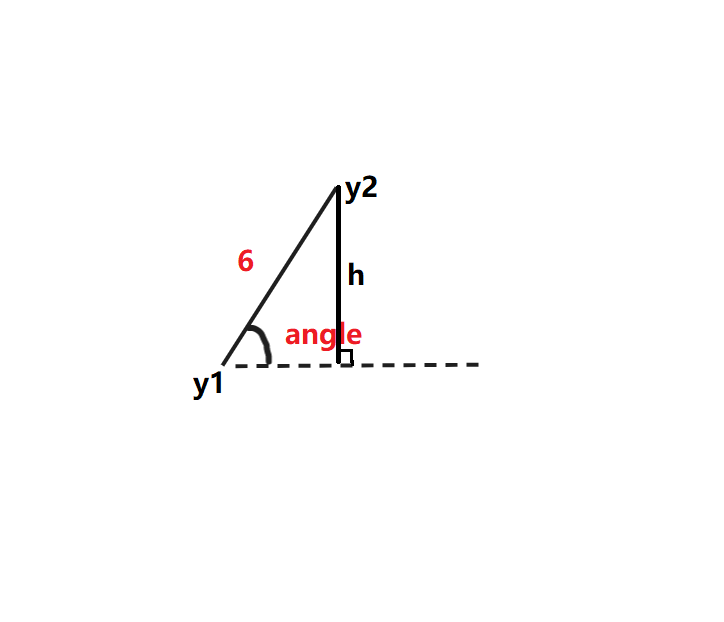
这里对angle的定义为：

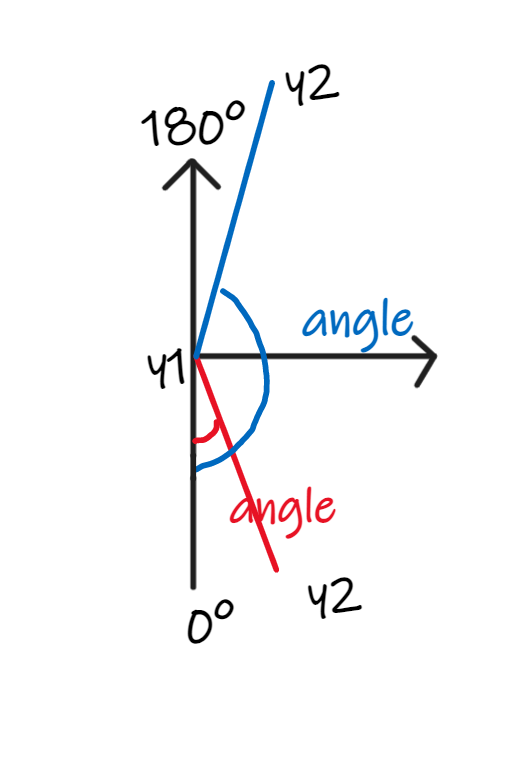
根据一点简单的三角函数，我们可以知道：

所以通过y1计算y2的方法就是（这里用了一开始定义的inRange函数：

1
2
3
4
if inRange(self.angle, 0, 90):
    self.coords[2] = self.coords[1] - math.sin(math.radians(90 - self.coords[0])) * 6
elif inRange(self.angle, 91, 180):
    self.coords[2] = self.coords[1] + math.sin(math.radians(self.coords[0] - 90)) * 6

所以完整的__init__()函数就如下：

1
2
3
4
5
6
7
8
9
10
class Pin:
    def __init__(self) -> None:
        # [0]: angle [1]: y1 [2]: y2
        self.coords = [random.randint(0, 180), random.randint(0, 120), None]
        self.angle = self.coords[0]

        if inRange(self.angle, 0, 90):
            self.coords[2] = self.coords[1] - math.sin(math.radians(90 - self.coords[0])) * 6
        elif inRange(self.angle, 91, 180):
            self.coords[2] = self.coords[1] + math.sin(math.radians(self.coords[0] - 90)) * 6

2.3 碰撞检测

在这个简化版的程序里面，我们只要写一个循环，判断这根针的y1和y2是否包含lineYlist中的某一项即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
    def checkCollide(self, y1: int, y2: int) -> bool:
self.collided = [False, False, False, False, False, False, False, False, False]
count = 0
for lineY in lineYlist:
    if inRange(lineY, y1, y2):
        self.collided[count] = True
    else:
        self.collided[count] = False
    count += 1

if True in self.collided:
    return True
else: 
    return False

我这里用的方法可能有点笨，用一个和lineYlist长度相同的列表来分别记录是否跟lineYlist中的每一项碰撞。最后再判断这个列表中是否有True（且理论上来说，只能有一个）即可。

2.4 主循环与完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
# -*-Coding:UTF-8-*-
import math, random

lineYlist = [12, 24, 36, 48, 60, 72, 84, 96, 108]

def inRange(n, start, end = 0):
    return start <= n <= end if end >= start else end <= n <= start

print('''This is a Python program to get the approximate value of PI. It simulated the Buffon's needle problem 10 times by dropping 100000 needles each time.
Here we go...
''')

class Pin:
    def __init__(self) -> None:
        # [0]: angle [1]: y1 [2]: y2
        self.coords = [random.randint(0, 180), random.randint(0, 120), None]
        self.angle = self.coords[0]

        if inRange(self.angle, 0, 90):
            self.coords[2] = self.coords[1] - math.sin(math.radians(90 - self.coords[0])) * 6
        elif inRange(self.angle, 91, 180):
            self.coords[2] = self.coords[1] + math.sin(math.radians(self.coords[0] - 90)) * 6
        else:
            print('Some error occured when calculating y2!')

    def checkCollide(self, y1: int, y2: int) -> bool:
        self.collided = [False, False, False, False, False, False, False, False, False]
        count = 0
        for lineY in lineYlist:
            if inRange(lineY, y1, y2):
                self.collided[count] = True
            else:
                self.collided[count] = False
            count += 1

        if True in self.collided:
            return True
        else: 
            return False

for i in range(10):
    totalCollided = 0
    for x in range(100000):
        pin = Pin()
        ifCollided = pin.checkCollide(pin.coords[1], pin.coords[2])
        # print(pin.coords[0], pin.coords[1], pin.coords[2], ifCollided)
        if ifCollided:
            totalCollided += 1

    print(100000 / totalCollided)

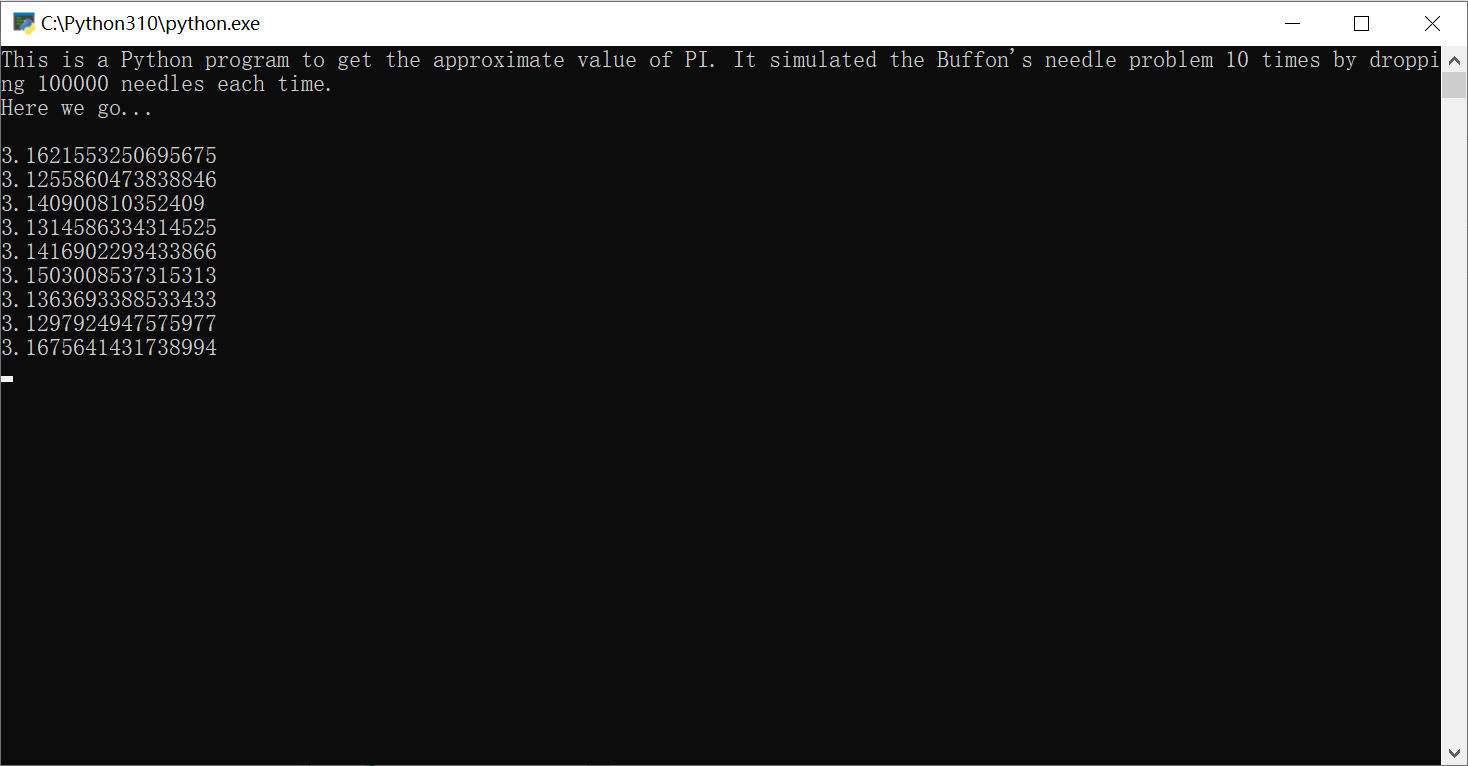
最后的话我们就循环10次，每次”投掷“100000根针并判断是否碰撞并计数。最后用次数100000除以碰撞次数即可。据测试，这种方法的精确度在十分位（即精确到3.1）。

3. 绘图版本的蒲丰投针

在这个版本里会更加复杂，既要模拟x坐标，也要模拟y坐标，且同时要判断碰撞和出界。绘图我先是用tkinter写了一遍，后来用pygame重写了一遍（而且比较复杂）。

3.1 tkinter版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
# -*-Coding:UTF-8-*-

# Preparing and Vars
import math, random, time
from tkinter import *

print('''This is a Python program to get the approximate value of PI. It simulated the Buffon's needle problem by dropping 1000 needles.
(With GUI this time!!!)
Here we go...
''')

lineYlist = [48, 96, 144, 192, 240, 288, 336, 384, 432, 480]

def inRange(n : int, start : int, end : float) -> bool:
    return start <= n <= end if end >= start else end <= n <= start

# Init the tkinter window
class Game:
    def __init__(self) -> None:
        self.tk = Tk()
        self.tk.title("Simulate Buffon's needle problem")
        self.tk.resizable(0, 0)
        self.tk.wm_attributes("-topmost", 1)
        self.canvas = Canvas(self.tk, width=1000, height=528, highlightthickness=0)
        self.canvas.pack()
        self.tk.update()
        self.running = True
        self.total = 0

    def mainloop(self) -> None:
        while self.running:
            self.tk.update_idletasks()
            self.tk.update()
            time.sleep(0.01)

class Sprite:
    def __init__(self, game):
        self.game = game
        self.coordinates = None
    def coords(self):
        return self.coordinates

class Coords:
    def __init__(self, x1=0, y1=0, x2=0, y2=0):
        self.x1 = x1
        self.y1 = y1
        self.x2 = x2
        self.y2 = y2

class ParaLine(Sprite):
    def __init__(self, game: Game, y: int) -> None:
        Sprite.__init__(self, game)
        self.y1 = self.y2 = y
        self.coordinates = Coords(0, y, 1000, y)
        game.canvas.create_line(self.coordinates.x1, self.coordinates.y1, self.coordinates.x2, self.coordinates.y2, fill="black")

class Needle(Sprite):
    def __init__(self, game: Game) -> None:
        Sprite.__init__(self, game)
        self.x1 = random.randint(0, 1000)
        self.y1 = random.randint(0, 528)
        self.angle = random.randint(0, 180)

        if inRange(self.angle, 0, 90):
            self.x2 = self.x1 - math.cos(math.radians(90 - self.angle)) * 24
        elif inRange(self.angle, 91, 180):
            self.x2 = self.x1 + math.cos(math.radians(self.angle - 90)) * 24

        if inRange(self.angle, 0, 90):
            self.y2 = self.y1 - math.sin(math.radians(90 - self.angle)) * 24
        elif inRange(self.angle, 91, 180):
            self.y2 = self.y1 + math.sin(math.radians(self.angle - 90)) * 24

        self.name = game.canvas.create_line(self.x1, self.y1, self.x2, self.y2, fill="black")

    def checkCollide(self, game: Game) -> bool:
        for lineY in lineYlist:
            if inRange(lineY, self.y1, self.y2):
                game.canvas.itemconfig(self.name, fill="red")
                game.total += 1
                return True
            else:
                pass

    def checkInside(self) -> bool:
        return True if inRange(self.x2, 0, 1000) and inRange(self.y2, 0, 528) else False


g = Game()
drawnLine = 0
collidedline = 0
for lineY in lineYlist:
    paraLine = ParaLine(g, lineY)
while drawnLine < 1000:
    needle = Needle(g)
    collided = needle.checkCollide(g)
    inside = needle.checkInside()
    if collided and inside:
        drawnLine += 1
        collidedline += 1
    elif (not collided) and inside:
        drawnLine += 1
    elif not inside:
        g.canvas.itemconfig(needle.name, fill='whitesmoke')

print(1000 / collidedline)
def on_closing():
    g.running = False

g.tk.protocol("WM_DELETE_WINDOW", on_closing)
g.mainloop()

其实基本的逻辑和纯输出版本差不多，只是需要初始化窗口且每一个元素都需要绘制，所以步骤多了一些。

3.2 Pygame版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
import pygame, math, random, time

print('''
This is a Python program to get the approximate value of PI. It simulated the Buffon's needle problem by dropping 1000 needles.
(With GUI this time!!!)
Here we go...
''')

lineYlist = [48, 96, 144, 192, 240, 288, 336, 384, 432, 480]

def inRange(n : int, start : int, end : float) -> bool:
    return start <= n <= end if end >= start else end <= n <= start

pygame.init()
screen = pygame.display.set_mode((1000,528))

class Needle():
    def __init__(self) -> None:
        self.x1 = random.randint(0, 1000)
        self.y1 = random.randint(0, 528)
        self.angle = random.randint(0, 180)

        if inRange(self.angle, 0, 90):
            self.x2 = self.x1 - math.cos(math.radians(90 - self.angle)) * 24
        elif inRange(self.angle, 91, 180):
            self.x2 = self.x1 + math.cos(math.radians(self.angle - 90)) * 24

        if inRange(self.angle, 0, 90):
            self.y2 = self.y1 - math.sin(math.radians(90 - self.angle)) * 24
        elif inRange(self.angle, 91, 180):
            self.y2 = self.y1 + math.sin(math.radians(self.angle - 90)) * 24

        self.name = pygame.draw.line(screen, (0,0,0), (self.x1, self.y1), (self.x2, self.y2))

    def checkCollide(self) -> bool:
        for lineY in lineYlist:
            if inRange(lineY, self.y1, self.y2):
                pygame.draw.line(screen, (255,0,0), (self.x1, self.y1), (self.x2, self.y2))
                return True
            else:
                pass

    def checkInside(self) -> bool:
        return True if inRange(self.x2, 0, 1000) and inRange(self.y2, 0, 528) else False

    def getCoords(self) -> list[tuple()]:
        return [(self.x1, self.y1), (self.x2, self.y2)]

startPosList = []
endPosList = []
needleList = []
drawnLine = collidedline = 0
while drawnLine <= 1000:
    n = Needle()
    collided = n.checkCollide()
    inside = n.checkInside()
    coords = n.getCoords()
    if collided and inside:
        drawnLine += 1
        collidedline += 1
        startPosList.append(coords[0])
        endPosList.append(coords[1])
        needleList.append(n)
    elif (not collided) and inside:
        drawnLine += 1
        startPosList.append(coords[0])
        endPosList.append(coords[1])
        needleList.append(n)
    elif not inside:
        pass

print(1000 / collidedline)

running = True
while running:
    for event in pygame.event.get():
        if event.type == pygame.QUIT:
            running = False

    screen.fill((255,255,255))

    color = 0,0,0
    width = 1
    for lineY in lineYlist:
        pygame.draw.line(screen,color,(0,lineY),(1000,lineY),width)

    for x in range(1000):
        currentNeedle = needleList[x]
        startPos = startPosList[x]
        endPos = endPosList[x]
        pygame.draw.line(screen,color,startPos,endPos,width)
        if currentNeedle.checkCollide():
            pygame.draw.line(screen,(255,0,0),startPos,endPos,width)

    pygame.display.update()
    pygame.display.set_caption('Buffon')

这个Pygame版本我个人觉得写的比较臃肿，由于为了避免掉绘制出界的针且因为Pygame和tkinter在主循环逻辑上的不同（tkinter可以边运行变更新画面，Pygame一定要全计算好再整体绘制），我先循环直到生成1000根合适的针，再绘制，但也没有找到更简单的方法。

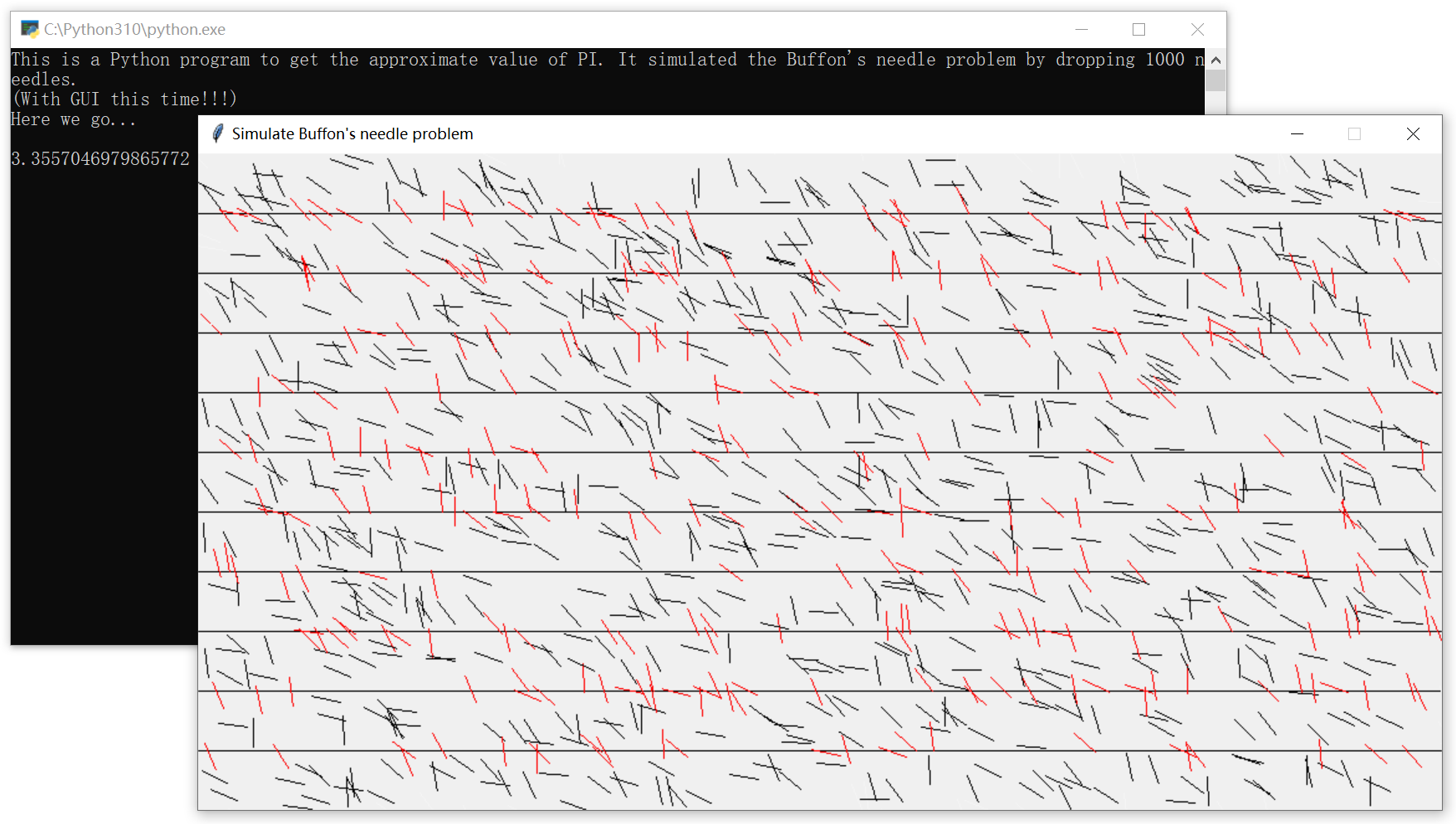
虽然这个程序还有一定的改进空间，但课程已经结束，我也不想再去改了（至少我逻辑是对的）。不过我还是想明白了一点，在写任何程序之前，一定要先捋清楚自己的思路，不然直接上手写，会很混乱、很复杂，甚至达不到自己想要的效果。

THE END感谢您的阅读~

相关文章 为你推荐
  • 2023-01-08
    生命游戏：在不确定中寻找确定

    “在不确定中寻找确定”，这是我的语文老师在2022年2月刚开始转线上课时对我们的一句嘱咐。如今，疫情尘埃落定，也据说再也不会有网课了。也许，这就是生命——不断前行、变幻莫测。

    但这两个词，又让我想起了另一种“生命”——康威生命游戏。这两天，灵机一动，我用Python实现了这“零玩家游戏”。

  • 2023-01-06
    漫谈密码学——不仅仅是password

    漫谈密码学，这是这个学期我研究性学习的主题。这次合作之路坎坎坷坷，中期报告和最后的结题报告分别因为活动和疫情取消了，但我也还是用心的写了几个有关加密的程序，最后的成绩也还不错。现在用这篇文章来做一个总结，也顺带再来“漫谈密码学”。

    漫谈的内容主要有，密码学的定义与历史，艾伦·图灵，和三类加密方式。我也会展示我写的四个程序，讲一讲当时的思路。

  • 2021-11-28
    【转】Markdown中Latex常用语法

    这篇文章是我转载过来的（很抱歉的是原网址已经找不到了），自己进行了一些格式上的修改。有些 $\LaTeX$标签可能显示不出来，同志们这是编译器的问题，因人而异……

    0. LaTeX 是什么？

    $ \LaTeX $是一种基于ΤeΧ的排版系统，由美国计算机学家莱斯利·兰伯特（Leslie Lamport）在20世纪80年代初期开发.
    利用这种格式，即使使用者没有排版和程序设计的知识也可以充分发挥由TeX所提供的强大功能，能在几天、甚至几小时内生成很多具有书籍质量的印刷品。
    对于生成复杂表格和数学公式，这一点表现得尤为突出。因此它非常适用于生成高印刷质量的科技和数学类文档。这个系统同样适用于生成从简单的信件到完整书籍的所有其他种类的文档。

赏作者一杯作业......

欢迎关注我的其它发布渠道